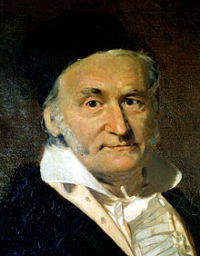
Карл Фридрих Гаусс — немецкий математик (30 апреля 1777 — 23 февраля 1855)

Карл Фридрих Гаусс родился 30 апреля 1777 года в Брауншвейге в семье водопроводчика.

Уже в детском возрасте проявил ярко выраженные математические способности. В 1795-1798 годах учился в Геттингенском университете. В 10-летнем возрасте решил задачу о суммировании чисел от 1 до 100, чем обратил на себя внимание учителя и тот начал заниматься с ним индивидуально. 30 марта 1796 решил задачу о построении правильного 17-угольника, что явилось поворотным пунктом в жизни Гаусса. Он решает посвятить себя не филологии, а исключительно математике.

С 1807 года — профессор математики и астрономии Геттингенского унниверситета и одновременно директор обсерватории. К концу учебы подготовил фундаментальную работу по теории чисел и высшей алгебре «Арифметические исследования».

Мировую известность Гаусс приобрел после разработки им метода вычисления эллиптической орбиты планеты по трем наблюдениям. Применение этого метода к малой планете Церера дало возможность вновь найти ее на небе после того, как она была утеряна вскоре после ее открытия Дж.Пиацци в 1801 году.

В фундаментальной работе «Теория движения небесных тел» (1809) Гаусс изложил методы вычисления планетных орбит, с небольшими усовершенствованиями используемые и в настоящее время.

Иностранный почетный член Петербургской АН с 1824 года. Его имя занесено на карту Луны.

Умер Карл Фридрих Гаусс 23 февраля 1855 года в Геттингене.